이런저런 IT 이야기
Programming Challenges #39 본문

The Stern-Brocot tree is a beautiful way for constructing the set of all nonnegative fractions m/n where m and n are relatively prime. The idea is to start with two fractions ( 0/1 , 1/0 ) and then repeat the following operations as many times as desired: Insert m+m′/n+n′ between two adjacent fractions m/n and m′/n′ . For example, the first step gives us one new entry between 0/1 and 1/0
Stern-Brocot 트리는 m과 n이 서로 소인 모든 음수가 아닌 분수 m/n을 생성하는 방법입니다. 아이디어는 두 개의 분수 (0/1, 1/0)로 시작하고, 다음 작업을 원하는 만큼 반복하는 것입니다: 인접한 분수 m/n과 m′/n′ 사이에 m+m′/n+n′을 삽입합니다. 예를 들어, 첫 번째 단계에서는 0/1과 1/0 사이에 새로운 항목이 하나 추가됩니다.
0/1 , 1/1 , 1/0
and the next gives two more
다음 단계에서는 두 개의 항목이 더 추가됩니다.
0/1 , 1/2 , 1/1 , 2/1 , 1/0 .
The next gives four more,
다음 단계에서는 더 네 개의 항목이 추가됩니다.
0/1 , 1/3 , 1/2 , 2/3 , 1/1 , 3/2 , 2/1 , 3/1 , 1/0
and then we will get 8, 16, and so on. The entire array can be regarded as an infinite binary tree structure whose top levels look like this
그리고 그 다음에는 8, 16과 같이 더 많은 항목들이 얻어집니다. 전체 배열은 이러한 형태로 보면 무한 이진 트리 구조로 간주될 수 있습니다.

The construction preserves order, and we couldn’t possibly get the same fraction in two different places. We can, in fact, regard the Stern-Brocot tree as a number system for representing rational numbers, because each positive, reduced fraction occurs exactly once. Let’s use the letters ‘L’ and ‘R’ to stand for going down to the left or right branch as we proceed from the root of the tree to a particular fraction; then a string of L’s and R’s uniquely identifies a place in the tree. For example, LRRL means that we go left from 1/1 down to 1/2 , then right to 2/3 , then right to 3/4 , then left to 5/7 . We can consider LRRL to be a representation of 5/7 . Every positive fraction gets represented in this way as a unique string of L’s and R’s. Well, actually there’s a slight problem: The fraction 1 1 corresponds to the empty string, and we need a notation for that. Let’s agree to call it I, because that looks something like 1 and it stands for “identity”. In this problem, given a positive rational fraction, you are expected to represent it in Stern-Brocot number system.
Stern-Brocot 트리는 순서를 보존하며 동일한 분수를 서로 다른 위치에서 얻을 수 없습니다. 실제로, Stern-Brocot 트리는 약분된 분수가 정확히 한 번씩 나타나는 수 체계로 간주할 수 있습니다. Stern-Brocot 수 체계에서는 'L'과 'R'이라는 문자를 사용하여 트리의 루트에서 특정 분수까지 이동할 때 왼쪽 또는 오른쪽 가지로 이동하는 것을 나타냅니다. 'L'과 'R'의 연속은 트리의 특정 위치를 고유하게 식별합니다. 예를 들어, 'LRRL' 문자열은 분수 5/7을 나타냅니다. 1/1에서 시작하여 왼쪽으로 1/2로 이동한 다음 오른쪽으로 2/3, 그리고 다시 오른쪽으로 3/4로 이동한 후 왼쪽으로 5/7로 이동합니다. 모든 양의 분수는 'L'과 'R'의 고유한 연속으로 이러한 방식으로 표현됩니다. 하지만 실제로는 약간의 문제가 있습니다. 분수 1/1은 빈 문자열에 해당하는데, 이를 표기하기 위해 'I'로 지정하기로 합의합니다. 'I'는 1과 비슷한 형태이며 "identity"를 나타내기 때문입니다. 이 문제에서는 주어진 양의 분수를 Stern-Brocot 수 체계로 표현해야 합니다.
Sample Input
5 7
878 323
1 1
Sample Output
LRRL
RRLRRLRLLLLRLRRR
결과코드
let lm, ln, rm, rn;
let m, n, p, q;
let track = '';
p = 5;
q = 7;
lm = 0;
ln = 1;
rm = 1;
rn = 0;
m = 1;
n = 1;
while (m != p || n != q) {
console.log(` p*n : ${p*n} | q*m : ${q*m}`)
if (p * n < q * m) {
track += 'L';
rm = m;
rn = n;
m = lm + rm;
n = ln + rn;
}else if(p * n > q * m){
track += 'R';
lm = m;
ln = n;
m = lm + rm;
n = ln + rn;
}
console.log(` m : ${m} | n : ${n}`)
}
console.log(track)
핵심내용
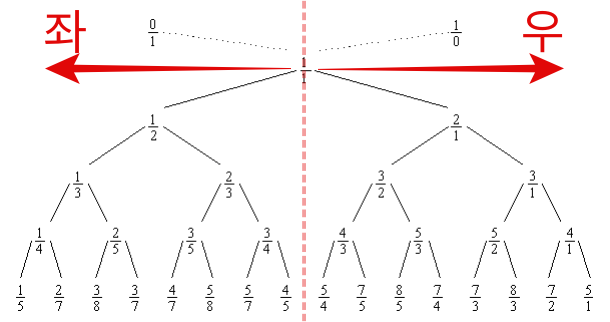
- 가장 중요한 핵심는 위 구조의 패턴입니다.
- 1/1을 기준으로 좌측은 기준 값보다 작고 우측은 기준 값보다 큽니다.
- 주어진 값을 찾아가면서 그 값의 위치를 좌측은 L로 우측은 R로 문자열을 추가 합니다.
- 찾아 가는 값들은 부모입니다. 그 부모들이 주어진 값보다 작으면 좌측 크면 우측으로 계속 찾아 값니다.
- 주어진값과 부모값의 비교는 유리수의 비교 방법중 곱하기 p/q ? m/n 비교입니다. p*n ? q*m 비교하는 방법으로 비교합니다.
- 결국 찾아가는 값들이 주어진 값과 같을때 종료 됩니다.
'Algorithm' 카테고리의 다른 글
| Programming Challenges #41 (0) | 2023.06.01 |
|---|---|
| Programming Challenges #40 (0) | 2023.05.31 |
| Programming Challenges #37 (0) | 2023.05.27 |
| 힙 정렬 알고리즘 (Heap Sort Algorithm) (1) | 2023.05.27 |
| 퀵 정렬 알고리즘 (Quick Sort Algorithm) (0) | 2023.05.27 |




